Density estimation with kernels
PDFs and parametric vs. non-parametric approaches
When analyzing a set of data, it may be useful to determine the underlying probabalistic process (assuming one exists) that generated said data. That is, assume for a data set
The function
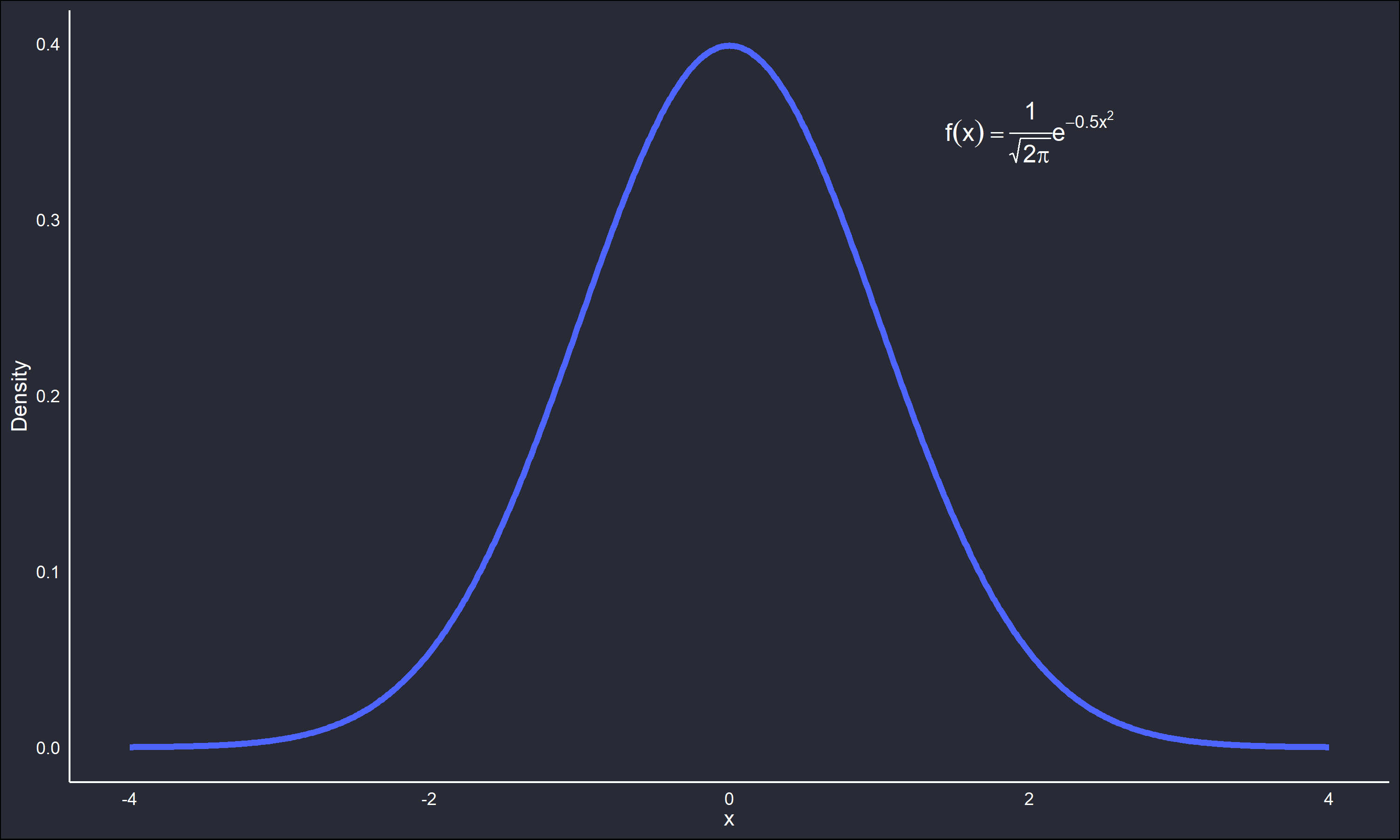
The scale parameter (variance) is 1 and the location parameter (mean) is 0. A set of data theorized to come from this distribution would have the majority of values about 0, and few outliers beyond the upper and lower tails.
How to obtain an estimate
The kernel approach
To better contextualize KDE, consider the histogram. A histogram is a tried and true method of data visualization, however it also can be thought of as a crude approximation of a PDF. Below is a histogram for 10,000 datapoints sampled from the previously mentioned normal distribution, with a bin width of 0.5 units.
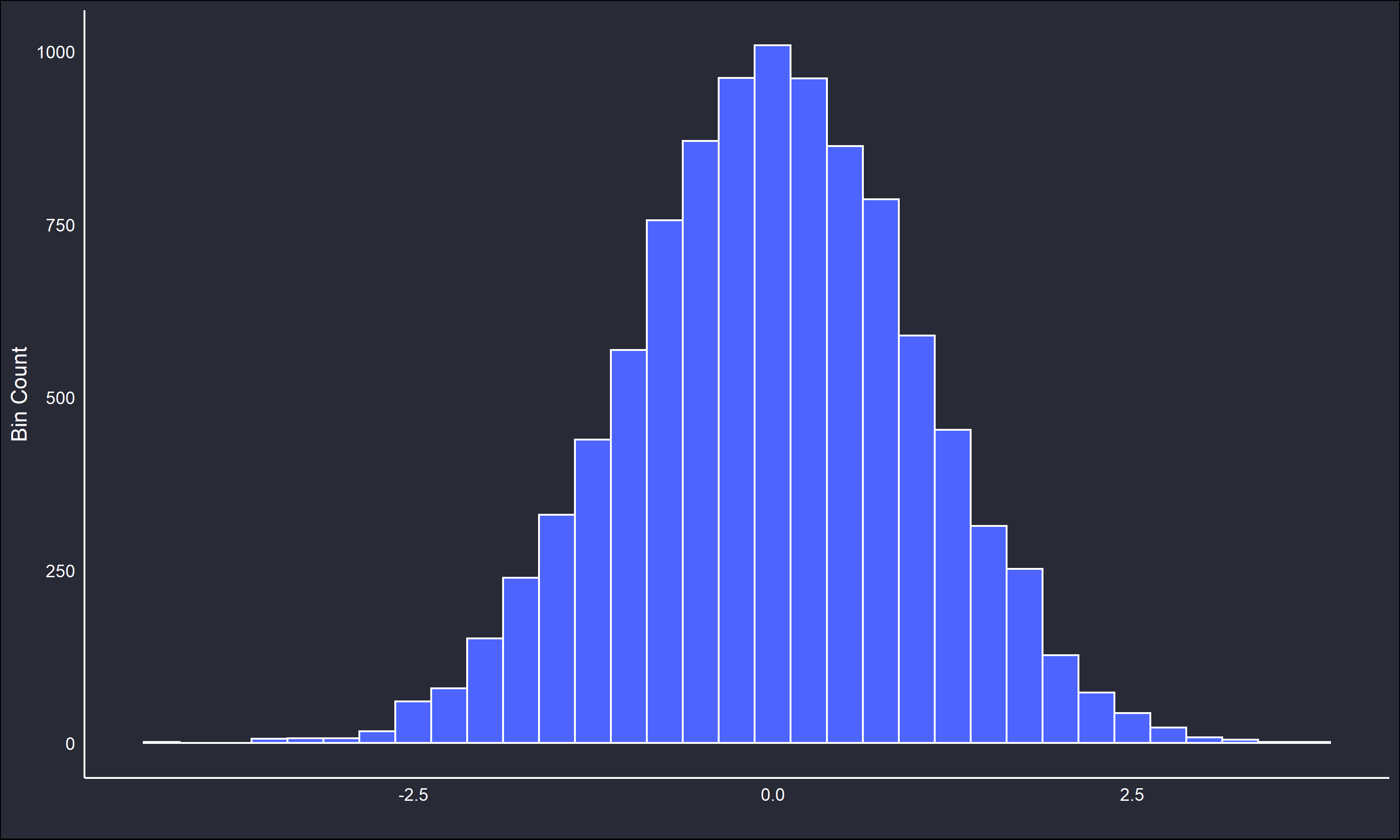
Note how the unimodality and symmetry from the standard normal PDF is reflected in the histogram. The histogram is an excellent tool for exploratory analysis, however it is not without shortcomings. Changing the bin width or origin may greatly affect the interpretation of the histogram. Further, the histogram as an estimate of a PDF is not mathematically suitable. The bin counts may be transformed into density estimates, however the underlying function has none of the properties of a PDF, for example differentiability and integration to unity. This can be problematic depending on the reasons for estimating
The KDE approach differs from the histogram to address these concerns. Instead of representing density by the proportion of data occupying a discrete set of bins of fixed width, an individual function is affixed to every data point. The individual curves are then summed together into a single smooth estimate of
where
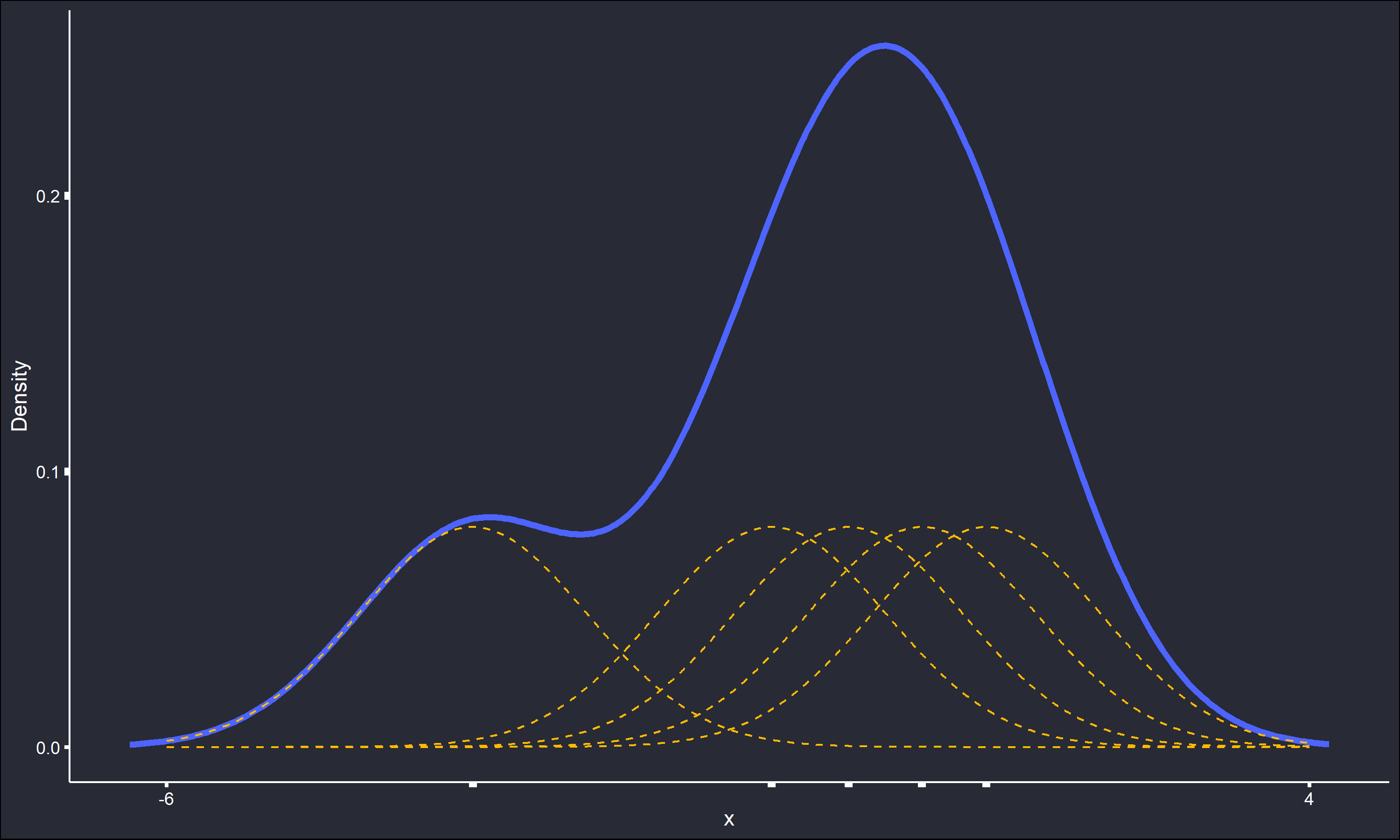
The
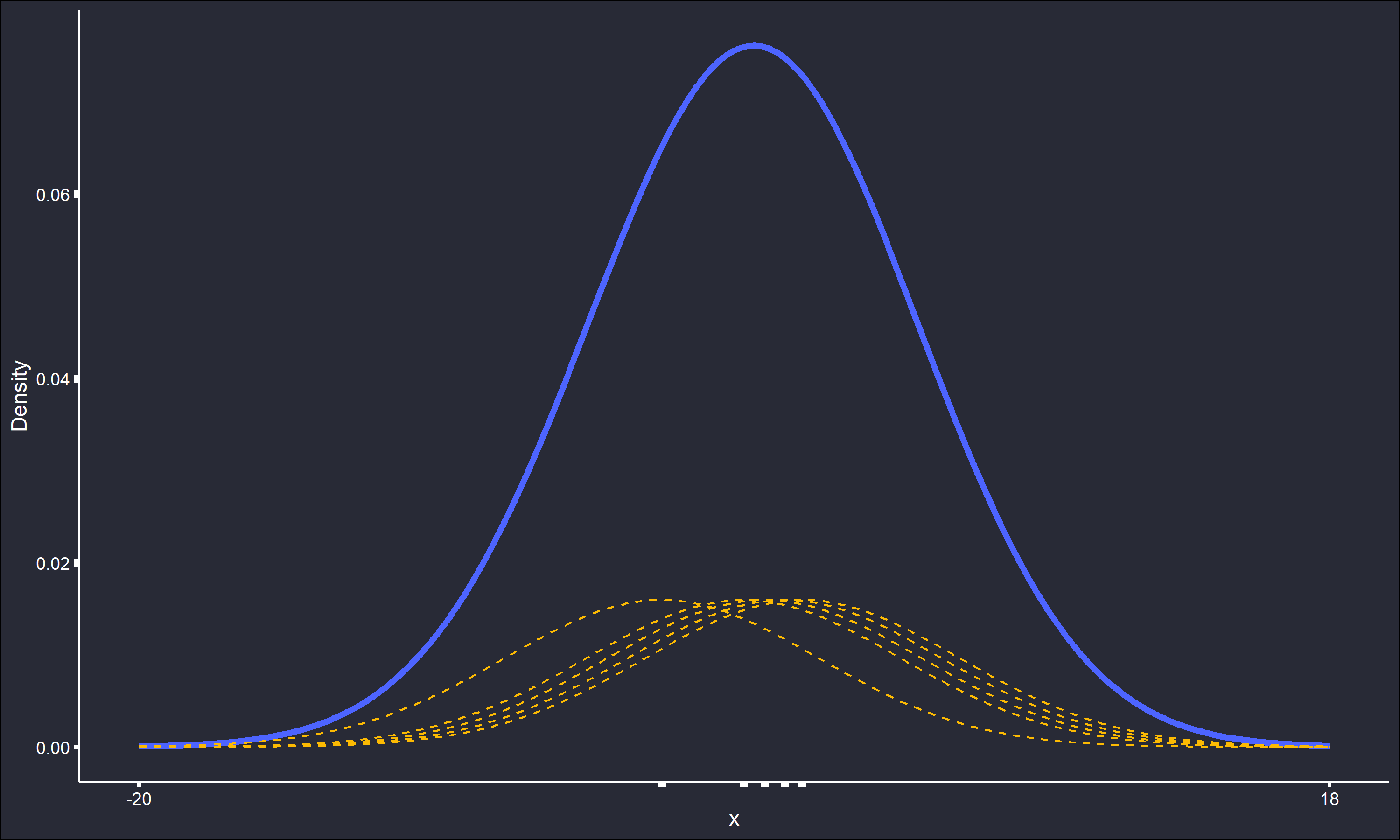
All the detail in the estimate has been smoothed out, and the absolute range of the estimate has also increased over 300%. Cleary the value of
There exist iterative methods for the “optimal” selection of
Note that straightforward KDE is not without it’s shortcomings. In particular, every data point is affixed with a kernel weighted and shaped the same regardless of the relative “closeness” of the data. That is, outliers or other information in the tails may be given too much importance in the final estimate. There do exist adaptive methods to address this issue that essentially let
KDE as explained here is a relatively simple process, but matters can become more complex. Either of the two sources I reccomended above would be a good way to become more aquainted with these details. I hope this post serves as a good starting point to this useful topic.